Miller 调制副载波及频谱、功率谱计算

Miller编码图 ​

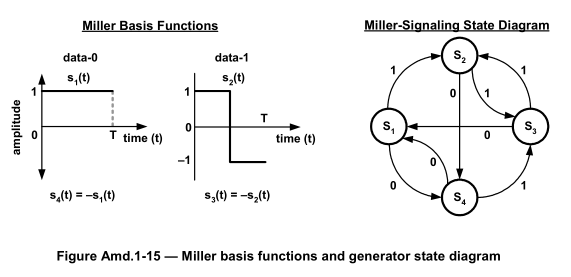
1. Miller基函数:

   • 图像左侧部分展示了两个波形，每个波形代表如何在时间轴上表示二进制数据0和1。

   • 当数据是1时，波形 $s2(t)$ 在整个周期T内保持不变，不会在周期中间翻转。

   • 当数据是0时，波形 $s1(t)$ 在周期T的一半时刻处于0幅度，并在周期中间翻转。

   • 图中还展示了 $s3(t)$ 和 $s4(t)$ 的关系，表明它们是 $s1(t)$ 和 $s2(t)$ 的相反数。这意味着信号的幅度是相反的。

2. Miller信号状态图:

   • 图像右侧部分是一个状态转换图，表明了Miller编码的四种状态 $S1, S2, S3,$ 和 $S4$ 之间的转换。

   • 状态之间的箭头标有0或1，表示如果在给定状态接收到一个0或1，信号将转移到哪个新状态。

   • 比如，从状态 S1 开始，如果接收到1，它将转移到 S2；如果接收到0，它将转移到 S4。

   • 这个状态图有助于理解在连续接收到一串二进制数据时，Miller编码如何在不同的状态间转换，以生成最终的编码信号。

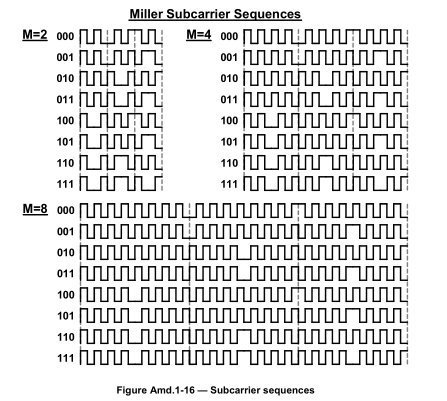
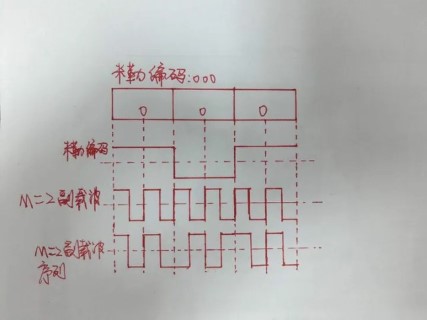
Miller调制副载波 ​

• 副载波编码就是用副载波的波形乘原波形，得到的就是编码后的波形。

频谱、功率谱 ​

频谱（Spectral Analysis）: ​

1. 连续信号的频谱

   对于连续时间信号 $x(t)$，其频谱可以通过傅里叶变换（FT）计算得到：

   $X(f) = int_{-\infty}^{+\infty} x(t)e^{-j2\pi ft}dt$

   这里，$X(f)$ 是信号 $x(t)$ 在频域的表示，$f$ 是频率。

2. 离散信号的频谱

   对于离散时间信号 $x[n]$，使用离散傅里叶变换（DFT）：

   $X[k] = \sum_{n=0}^{N-1} x[n]e^{-j2\pi \frac{kn}{N}}$

   其中，$N$ 是信号样本的总数，$k$ 是离散频率指标。

功率谱求解 ​

1. 连续信号的功率谱密度

   对于连续信号 $x(t)$，其功率谱密度可以通过以下步骤计算得到：

   1. 计算自相关函数：首先，计算信号的自相关函数 $R(\tau)$，这是信号与其自身延迟版本的卷积：

      $R(\tau) = \int_{-\infty}^{\infty} x(t)x(t+\tau)dt$

      自相关函数提供了信号在不同时间延迟下的相似性度量。

   2. 傅里叶变换自相关函数：然后，对自相关函数进行傅里叶变换以获得功率谱密度 $P(f)$：

      $P(f) = \int_{-\infty}^{\infty} R(\tau)e^{-j2\pi f\tau}d\tau$

      这个变换将自相关函数从时间域转换到频率域，提供了信号功率如何分布在不同频率上的视图。

2. 离散信号的功率谱密度

   对于离散信号 $x[n]$，功率谱密度的计算略有不同：

   1. 周期图法：这是一种直接方法，通过计算信号的离散傅里叶变换（DFT）的模的平方来估计功率谱：

      $P[k] = |X[k]|^2$

      其中 $X[k]$ 是信号 $x[n]$ 的DFT。这种方法简单直接，但可能不适用于所有类型的信号，尤其是那些非平稳信号。

   2. Welch方法：这是一种改进的周期图法，通过将信号分割成重叠的段，对每段应用窗函数，然后计算每段的DFT，最后对所有段的功率谱取平均。这种方法可以减少估计的方差，改善对于非平稳信号的处理：

      1. 将信号分割成多个重叠的段。

      2. 对每个段应用窗函数（如汉宁窗）。

      3. 计算每个窗口化段的DFT，然后计算其模的平方以得到功率谱。

      4. 对所有段的功率谱取平均，得到最终的功率谱密度估计。